题目:https://leetcode-cn.com/problems/predict-the-winner/
代码:
class Solution {
public boolean PredictTheWinner(int[] nums) {
int length = nums.length;
//偶数长度下先手玩家必赢
if (length % 2 == 0) {
return true;
}
//进行动态规划求解
int[][] dp = new int[length][length];
for (int i = 0; i < length; i++) {
dp[i][i] = nums[i];
}
for (int i = length - 2; i >= 0; i--) {
for (int j = i+1; j < length; j++) {
dp[i][j] = Math.max(nums[i] - dp[i + 1][j], nums[j] - dp[i][j - 1]);
}
}
return dp[0][length - 1] >= 0;
}
}
第一次做动态规划的题目,没解出来。上述代码是看了题解之后写出来的。
首先题目意思是给出一个数组,两个玩家轮流选取数字,选中什么数字就给自己加多少分,只能从开头或者结尾选,直到数组被选完。最后看谁分数大谁就赢。问在每个玩家都很聪明的情况下,玩家1先手能否必赢。
理解了题目意思之后看代码,上述代码中有2大部分:
一、数组个数为偶数:
这种情况下如不考虑求分数的话,则不需要去计算。先手玩家必赢,原因是什么呢?且看如下分析:
假设数组的值为:[1, 5, 233, 7],那么每个数字的下标为:[0, 1, 2, 3],刚好2个偶数下标和2个奇数下标。假设先手玩家选取了开头即0下标数字,后手玩家能选取的只能是1下标或者3下标,发现了吗,是奇数下标,没有其他选择。这个时候无论后手玩家选择了哪个数,再次轮到先手玩家的时候,先手玩家一定可以再次选择偶数下标的位置。以此类推,我们可以发现,只要先手玩家愿意,先手玩家可以在整场游戏中只选取偶数下标的数字,同理也可以只选取奇数下标,这取决于先手玩家是第一次选择是先选开头还是结尾。
有了上述的条件,我们可以通过下标的奇偶性把数组分成2部分并计算他们的分值:偶数下标T1:1+233=234,奇数下标T2:5+7=13。又因为T1+T2=total(所有数字的总分),这个时候我们可以发现,T1和T2之间只有3种情况,T1>T2 T1=T2 T1<T2。因为题目规定,如果最后分值相等,也算玩家1获胜,所以玩家1先手只需要在游戏开始之时,计算出T1和T2的值,根据T1和T2哪个值大来决定都选偶数下标的数字还是奇数下标的数字即可。综上所述,在偶数个数的情况下,先手玩家必赢,压根无需计算。
二、数组个数为奇数:
这种情况下,只能中规中矩的去分析和计算解答。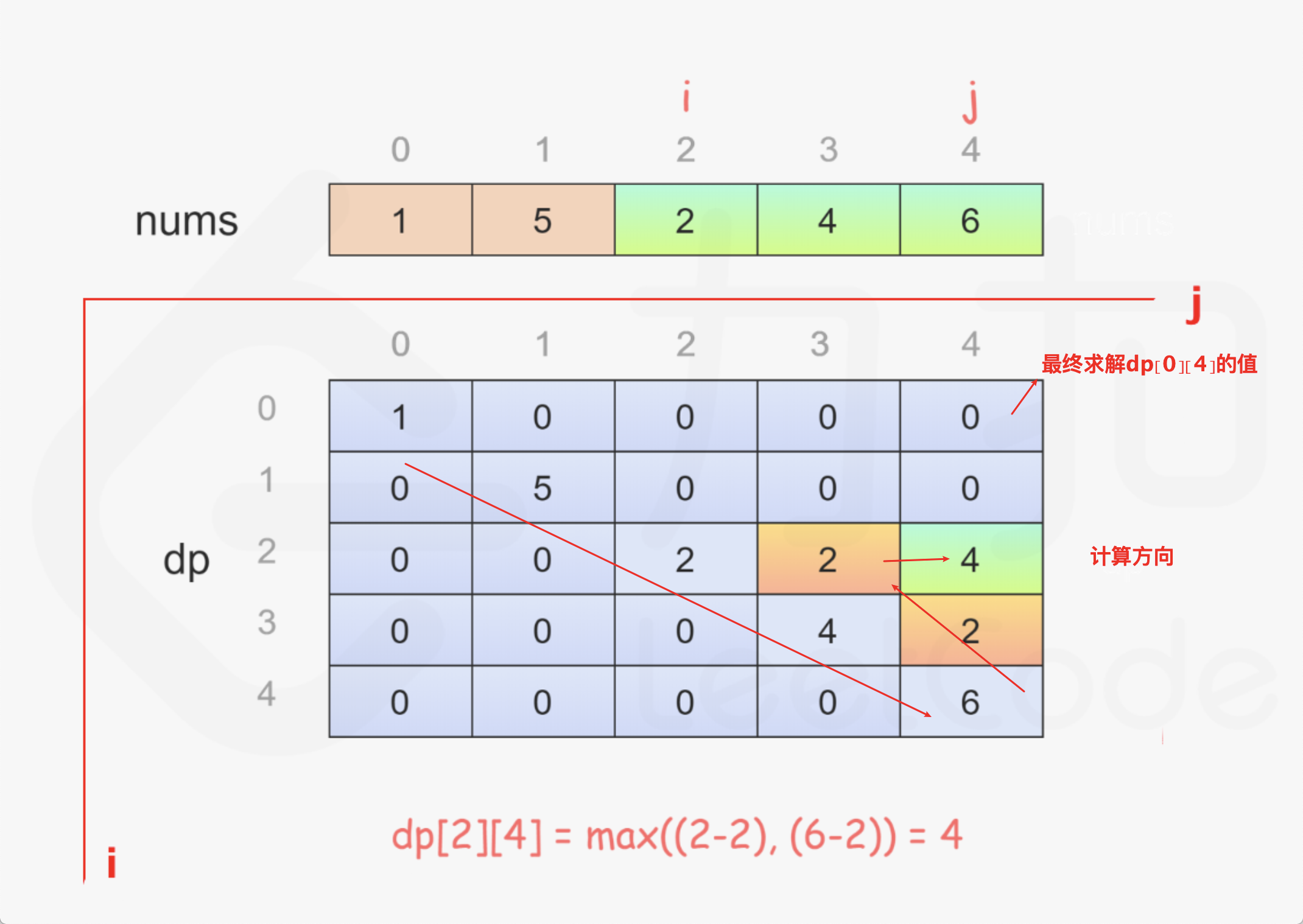
如图,我们定义一个二维数组dp,行列都为数组的长度。这个时候我们需要理解表格中每个格子中数字的含义,即dp[i][j]中值代表这什么:dp[i][j]的值代表,在i-j这个范围内的数字,我(先手)和对手经过各自的最优选择之后,我能领先的分数。注意这里的先手不考虑全局的范围,就考虑在i-j的范围内。也可以理解为,把原先的大数组,拆成多个i-j的小数组,每个小数组的情况都去计算结果,提前将结果缓存下来,避免使用递归方法调用时带来的重复计算。
了解了dp[i][j]值的含义之后,我们需要知道值的计算方法。
当i=j的时候,即只有一个数的情况下,那么先手玩家只能选择这个数,后手玩家没得选。所以dp[i][j]=dp[i][i]=nums[i],由此我们可以计算出表格中对角线的部分。
因不考虑i>j的情况,所以表格中对角线下方即左下角的部分值不计算,即为默认的0,且没有任何作用。
当i<j的时候,先手玩家只有两种选择,选择nums[i]或者nums[j],当选择nums[i]时,先手玩家可以领先分数为(当前选择的分数减去剩下的数组中最优解下能领先的分数):nums[i]-dp[i+1][j],当选择nums[j]时,先手玩家可以领先分数为:nums[j]-dp[i][j-1]。此时先手玩家选择i还是j位置的数字取决于上述计算的2个分数哪个大,所以可以得出dp[i][j]=max(nums[i]-dp[i+1][j],nums[j]-dp[i][j-1])。这个公式比较难理解,也是重点所在,可以多理解一会。
因为公式中的计算,会使用到dp的值,仔细看的话你会发现有点类似于递归函数。所以我们在计算整个dp表格的值的时候,按照图中箭头所示的顺序去计算。
综上,我们最终表格右上角即dp[0][length-1]的值如果大于等于0就代表着先手玩家1必赢。


