题目:https://leetcode-cn.com/problems/fibonacci-number/
代码:
方法一:递归
class Solution {
public int fib(int N) {
if(N<=1){
return N;
}
return fib(N-1)+fib(N-2);
}
}
递归是最简单的一个解法,但是性能上不行,因为会有很多重复的计算,比如计算fib(5),就要重复的调用5次fib(1),性能严重浪费。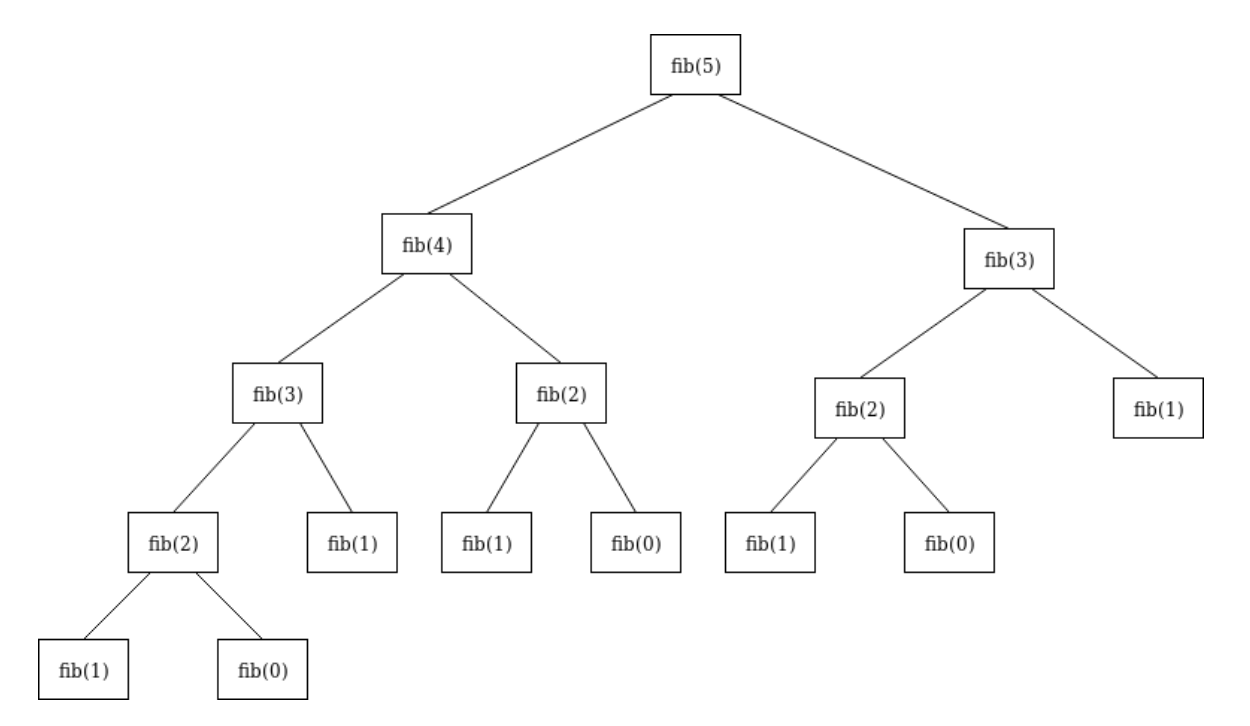
方法二:循环
class Solution {
public int fib(int N) {
if(N<=1){
return N;
}
int[] num = new int[N + 1];
num[0] = 0;
num[1] = 1;
for (int i=2; i <= N; i++) {
num[i] = num[i - 1] + num[i - 2];
}
return num[N];
}
}
使用一个数组存储数据,第i个数的值就等于第i-1和第i-2的值之和。相比第一种递归的方法减少了大量重复的计算。
方法三:带缓存的循环
class Solution {
private static int[] cache = new int[]{0, 1};
public int fib(int N) {
int i = cache.length;
if (N >= i) {
cache = Arrays.copyOf(cache, N + 1);
for (; i <= N; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
}
return cache[N];
}
}
方法三是方法二的优化版本,通过将数组缓存起来的方式,实现多次调用fib函数时性能上的提升,避免每一次都去计算。但是此方法会有并发的线程安全问题(这里暂不考虑,考虑的话方法加锁即可)
方法四:数学解法
采用各种数学公式直接计算值,具体参考百度。


